Gk
0%

EDA Practice on House Price Dataset (Kaggle)

Posted on Edited on

https://www.kaggle.com/ekami66/detailed-exploratory-data-analysis-with-python/data#Exploratory-data-analysis-(EDA)

Note: I do not own the codes below. This is identical to the codes from the above URL and is just used for practicing EDA.


Preparations

1
plt.style.use('bmh')
1
2
df = pd.read_csv('train.csv')
df.head()

Id MSSubClass MSZoning LotFrontage LotArea Street Alley LotShape LandContour Utilities ... PoolArea PoolQC Fence MiscFeature MiscVal MoSold YrSold SaleType SaleCondition SalePrice
0 1 60 RL 65.0 8450 Pave NaN Reg Lvl AllPub ... 0 NaN NaN NaN 0 2 2008 WD Normal 208500
1 2 20 RL 80.0 9600 Pave NaN Reg Lvl AllPub ... 0 NaN NaN NaN 0 5 2007 WD Normal 181500
2 3 60 RL 68.0 11250 Pave NaN IR1 Lvl AllPub ... 0 NaN NaN NaN 0 9 2008 WD Normal 223500
3 4 70 RL 60.0 9550 Pave NaN IR1 Lvl AllPub ... 0 NaN NaN NaN 0 2 2006 WD Abnorml 140000
4 5 60 RL 84.0 14260 Pave NaN IR1 Lvl AllPub ... 0 NaN NaN NaN 0 12 2008 WD Normal 250000

5 rows × 81 columns


1
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1460 entries, 0 to 1459
Data columns (total 81 columns):
 #   Column         Non-Null Count  Dtype  
---  ------         --------------  -----  
 0   Id             1460 non-null   int64  
 1   MSSubClass     1460 non-null   int64  
 2   MSZoning       1460 non-null   object 
 3   LotFrontage    1201 non-null   float64
 4   LotArea        1460 non-null   int64  
 5   Street         1460 non-null   object 
 6   Alley          91 non-null     object 
 7   LotShape       1460 non-null   object 
 8   LandContour    1460 non-null   object 
 9   Utilities      1460 non-null   object 
 10  LotConfig      1460 non-null   object 
 11  LandSlope      1460 non-null   object 
 12  Neighborhood   1460 non-null   object 
 13  Condition1     1460 non-null   object 
 14  Condition2     1460 non-null   object 
 15  BldgType       1460 non-null   object 
 16  HouseStyle     1460 non-null   object 
 17  OverallQual    1460 non-null   int64  
 18  OverallCond    1460 non-null   int64  
 19  YearBuilt      1460 non-null   int64  
 20  YearRemodAdd   1460 non-null   int64  
 21  RoofStyle      1460 non-null   object 
 22  RoofMatl       1460 non-null   object 
 23  Exterior1st    1460 non-null   object 
 24  Exterior2nd    1460 non-null   object 
 25  MasVnrType     1452 non-null   object 
 26  MasVnrArea     1452 non-null   float64
 27  ExterQual      1460 non-null   object 
 28  ExterCond      1460 non-null   object 
 29  Foundation     1460 non-null   object 
 30  BsmtQual       1423 non-null   object 
 31  BsmtCond       1423 non-null   object 
 32  BsmtExposure   1422 non-null   object 
 33  BsmtFinType1   1423 non-null   object 
 34  BsmtFinSF1     1460 non-null   int64  
 35  BsmtFinType2   1422 non-null   object 
 36  BsmtFinSF2     1460 non-null   int64  
 37  BsmtUnfSF      1460 non-null   int64  
 38  TotalBsmtSF    1460 non-null   int64  
 39  Heating        1460 non-null   object 
 40  HeatingQC      1460 non-null   object 
 41  CentralAir     1460 non-null   object 
 42  Electrical     1459 non-null   object 
 43  1stFlrSF       1460 non-null   int64  
 44  2ndFlrSF       1460 non-null   int64  
 45  LowQualFinSF   1460 non-null   int64  
 46  GrLivArea      1460 non-null   int64  
 47  BsmtFullBath   1460 non-null   int64  
 48  BsmtHalfBath   1460 non-null   int64  
 49  FullBath       1460 non-null   int64  
 50  HalfBath       1460 non-null   int64  
 51  BedroomAbvGr   1460 non-null   int64  
 52  KitchenAbvGr   1460 non-null   int64  
 53  KitchenQual    1460 non-null   object 
 54  TotRmsAbvGrd   1460 non-null   int64  
 55  Functional     1460 non-null   object 
 56  Fireplaces     1460 non-null   int64  
 57  FireplaceQu    770 non-null    object 
 58  GarageType     1379 non-null   object 
 59  GarageYrBlt    1379 non-null   float64
 60  GarageFinish   1379 non-null   object 
 61  GarageCars     1460 non-null   int64  
 62  GarageArea     1460 non-null   int64  
 63  GarageQual     1379 non-null   object 
 64  GarageCond     1379 non-null   object 
 65  PavedDrive     1460 non-null   object 
 66  WoodDeckSF     1460 non-null   int64  
 67  OpenPorchSF    1460 non-null   int64  
 68  EnclosedPorch  1460 non-null   int64  
 69  3SsnPorch      1460 non-null   int64  
 70  ScreenPorch    1460 non-null   int64  
 71  PoolArea       1460 non-null   int64  
 72  PoolQC         7 non-null      object 
 73  Fence          281 non-null    object 
 74  MiscFeature    54 non-null     object 
 75  MiscVal        1460 non-null   int64  
 76  MoSold         1460 non-null   int64  
 77  YrSold         1460 non-null   int64  
 78  SaleType       1460 non-null   object 
 79  SaleCondition  1460 non-null   object 
 80  SalePrice      1460 non-null   int64  
dtypes: float64(3), int64(35), object(43)
memory usage: 924.0+ KB
1
2
3
4
5
6
7
8
9
10
11
# df.count() does not include NaN values
# remove Id and the features with 30% or less NaN values
df2 = df[[column for column in df if df[column].count() / len(df) >= 0.3]]
del df2['Id']
print("List of dropped columns:", end=" ")
for c in df.columns:
    if c not in df2.columns:
        print(c, end=", ")

print('\n')
df = df2
List of dropped columns: Id, Alley, PoolQC, Fence, MiscFeature,

​ 

1
2
3
4
# the distribution of the housing price
print(df['SalePrice'].describe())
plt.figure(figsize=(9, 8))
sns.distplot(df['SalePrice'], color='g', bins=100, hist_kws={'alpha': 0.4});
count      1460.000000
mean     180921.195890
std       79442.502883
min       34900.000000
25%      129975.000000
50%      163000.000000
75%      214000.000000
max      755000.000000
Name: SalePrice, dtype: float64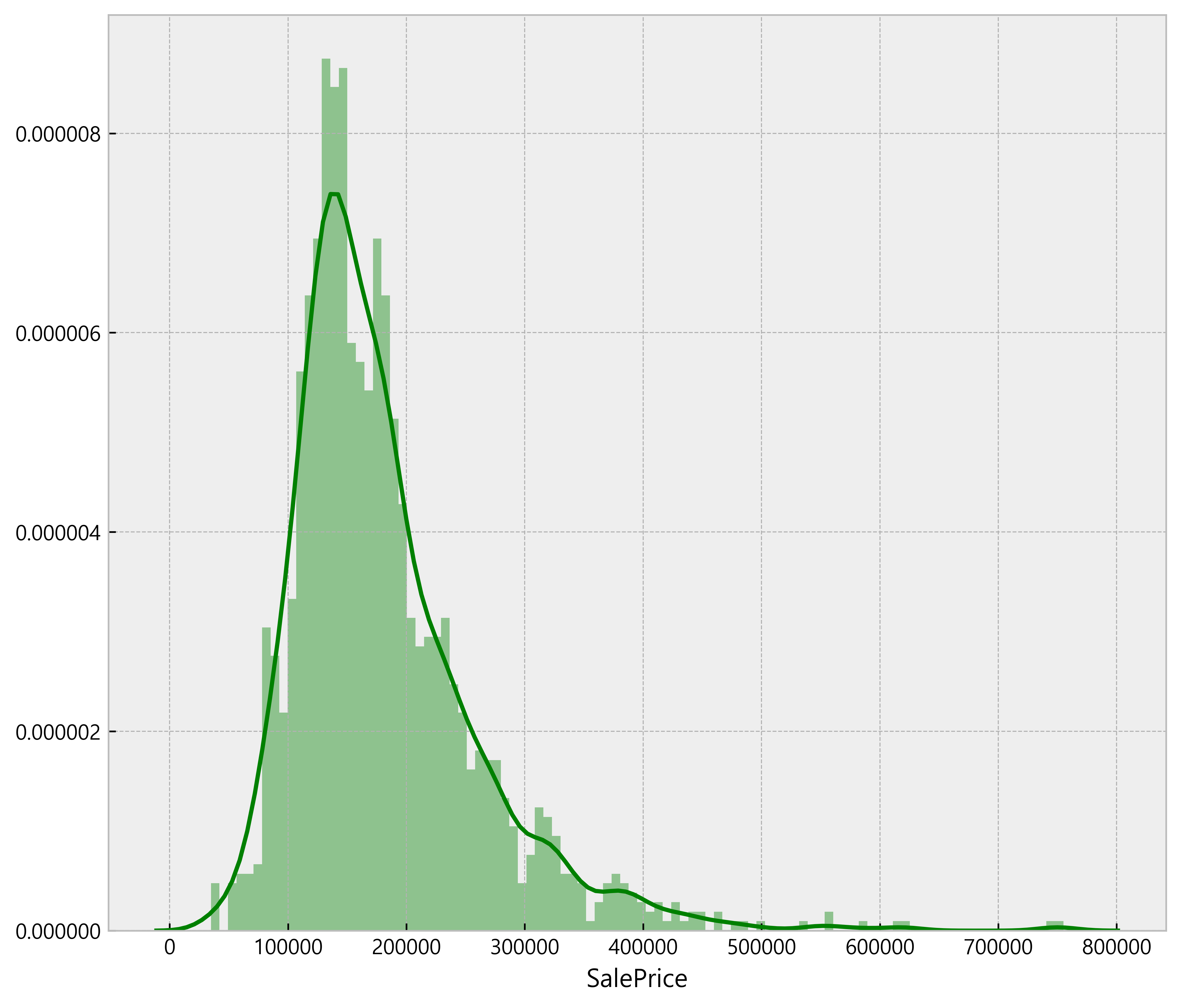

EDA_Practice_-_HousePrices_6_1

From the above graph, it can be deduced that there are outliers existing above $500,000. These outliers will be deleted to get a normal distribution of the independent variabl ('SalePrice') for machine learning <= (not sure what this means)


Numerical Data Distribution

1
list(set(df.dtypes.tolist()))
[dtype('O'), dtype('float64'), dtype('int64')]
1
2
df_num = df.select_dtypes(include = ['float64', 'int64'])
df_num.head()

MSSubClass LotFrontage LotArea OverallQual OverallCond YearBuilt YearRemodAdd MasVnrArea BsmtFinSF1 BsmtFinSF2 ... WoodDeckSF OpenPorchSF EnclosedPorch 3SsnPorch ScreenPorch PoolArea MiscVal MoSold YrSold SalePrice
0 60 65.0 8450 7 5 2003 2003 196.0 706 0 ... 0 61 0 0 0 0 0 2 2008 208500
1 20 80.0 9600 6 8 1976 1976 0.0 978 0 ... 298 0 0 0 0 0 0 5 2007 181500
2 60 68.0 11250 7 5 2001 2002 162.0 486 0 ... 0 42 0 0 0 0 0 9 2008 223500
3 70 60.0 9550 7 5 1915 1970 0.0 216 0 ... 0 35 272 0 0 0 0 2 2006 140000
4 60 84.0 14260 8 5 2000 2000 350.0 655 0 ... 192 84 0 0 0 0 0 12 2008 250000

5 rows × 37 columns


Plot them all:

1
df_num.hist(figsize=(15, 20), bins=50, xlabelsize=8, ylabelsize=8);

EDA_Practice_-_HousePrices_12_0


“Features such as 1stFlrSF, TotalBsmtSF, LotFrontage, GrLiveArea… seems to share a similar distribution to the one we have with SalePrice. Lets see if we can find new clues later.”

At this point, I suddenly came to wonder what are we trying to find through all this process? Why does it seem like the SalePrice is the center of the whole thing. 

1
2
3
df_num_corr = df_num.corr()['SalePrice'][:-1] # -1 because the last row is SalePrice
golden_features_list = df_num_corr[abs(df_num_corr) > 0.5].sort_values(ascending=False)
print("The following are the top {} strongly correlated values with SalePrice:\n{}".format(len(golden_features_list), golden_features_list))
The following are the top 10 strongly correlated values with SalePrice:
OverallQual     0.790982
GrLivArea       0.708624
GarageCars      0.640409
GarageArea      0.623431
TotalBsmtSF     0.613581
1stFlrSF        0.605852
FullBath        0.560664
TotRmsAbvGrd    0.533723
YearBuilt       0.522897
YearRemodAdd    0.507101
Name: SalePrice, dtype: float64

From the table above, we now know which data has the strongest relationship with the SalePrice. But, this data is still incomplete as the outliers still exist in the dataset.


To get rid of the outliers the following measures can be taken:

1
2
3
1. Plot the numerical features and see which ones have very few or explainable outliers

2. Remove the outliers from these features and see which one can have a good correlation without their outliers

NOTE 1

  • Correlation by itself does not always explain the relationship between data
  • Plotting data could lead to new insights

THEREFORE ALWAYS VISUALIZE THE DATA


NOTE 2

Through the correlation value,the curvilinear relationship cannot be deduced.

SO ALWAYS VISUALIZE THE DATA IN NUMEROUS WAYS TO GET MORE INSIGHTS

1
For example, relationships such as curvilinear relationship cannot be guessed just by looking at the correlation value so lets take the features we excluded from our correlation table and plot them to see if they show some kind of pattern.

Not sure yet what features were excluded from the correlation table.


1
2
3
4
5
for i in range(0, len(df_num.columns), 5):
    sns.pairplot(data=df_num,
                 x_vars=df_num.columns[i:i+5],
                 y_vars=['SalePrice']
                )

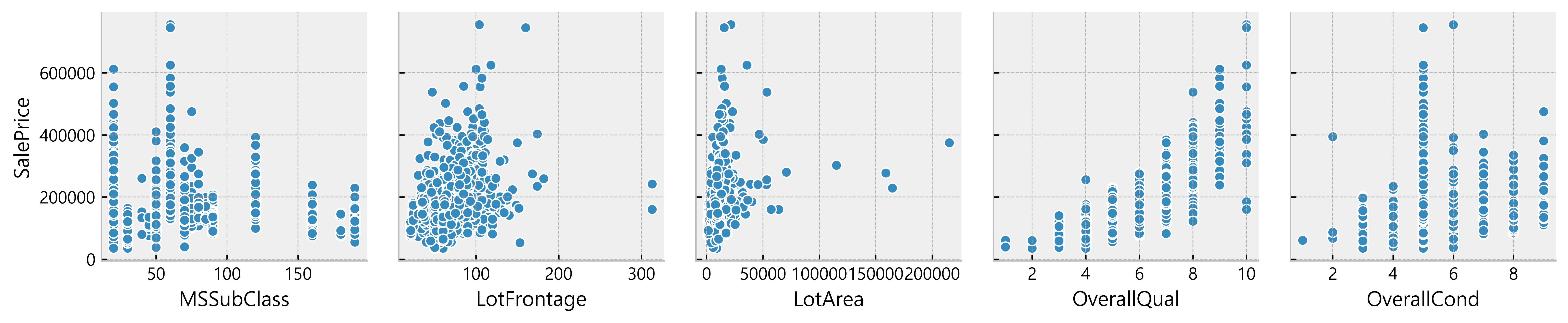
EDA_Practice_-_HousePrices_18_0

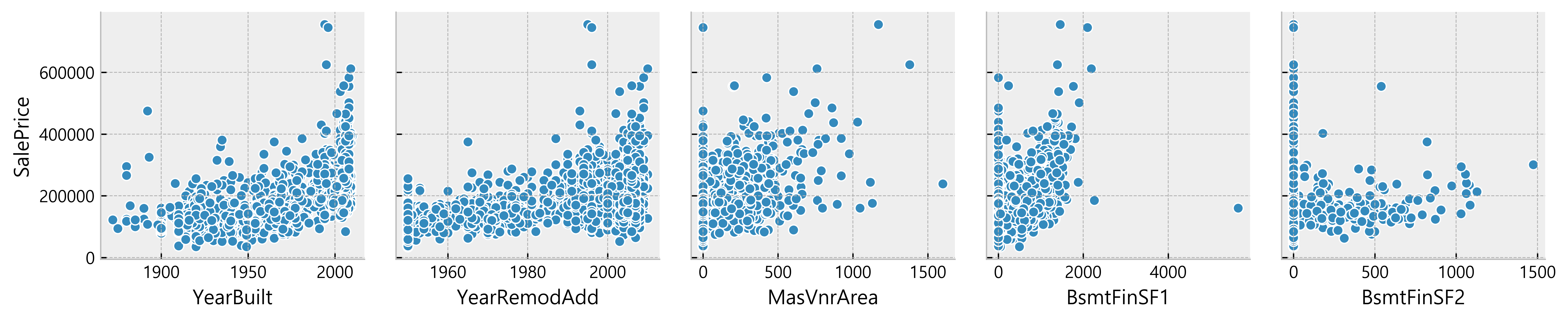
EDA_Practice_-_HousePrices_18_1

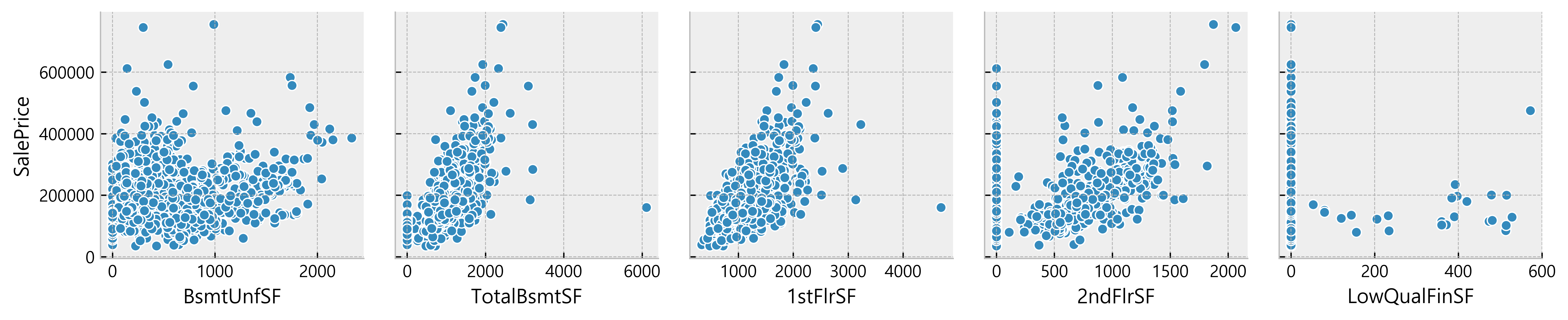
EDA_Practice_-_HousePrices_18_2

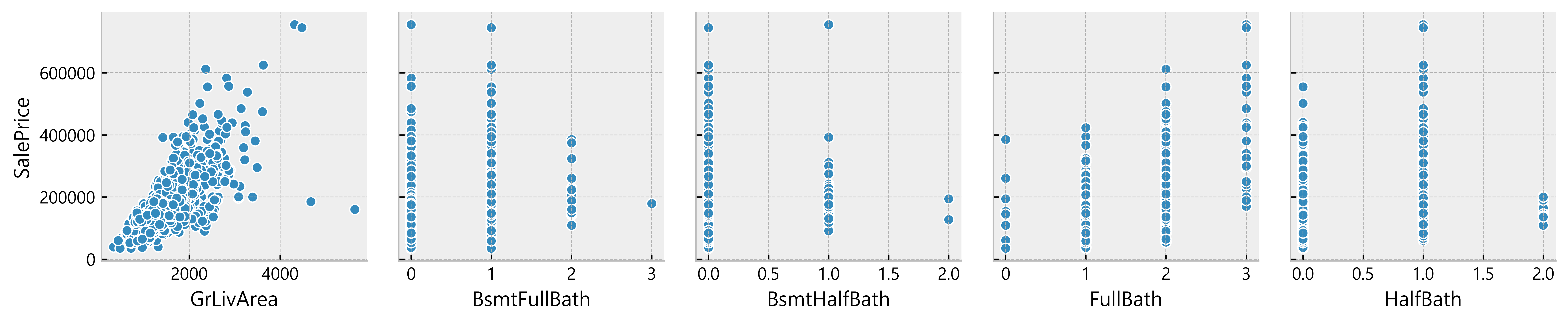
EDA_Practice_-_HousePrices_18_3

EDA_Practice_-_HousePrices_18_4

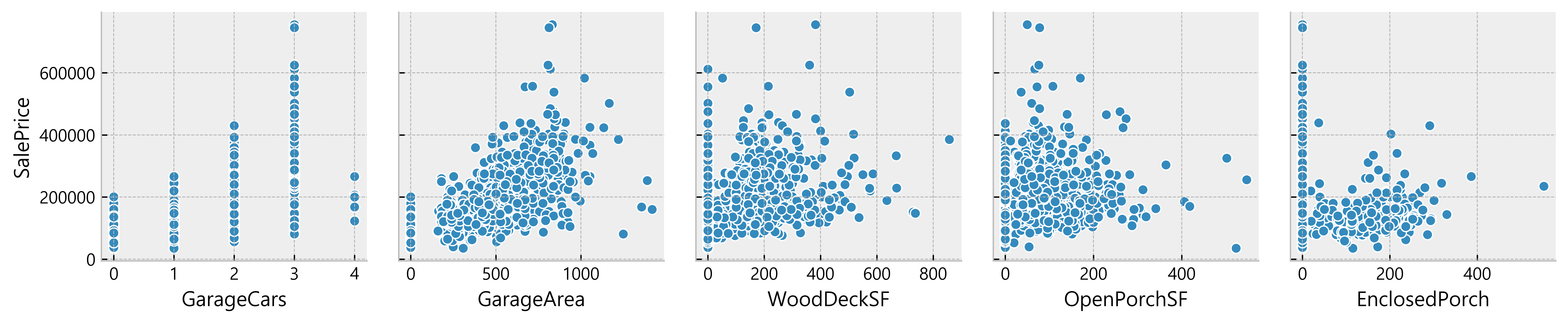
EDA_Practice_-_HousePrices_18_5

EDA_Practice_-_HousePrices_18_6

EDA_Practice_-_HousePrices_18_7


Deduction:

- Many data seem to have a linear relationship with the SalePrice
    - A lot of data points are located on x = 0 
  Possible indication of absence of such features in the house)

More Data Cleaning

Removal of 0 values and repeat the process of finding correlated values

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import operator

individual_features_df = []
for i in range(0, len(df_num.columns) - 1):
# -1 because the last column is SalePrice
    tmpDf = df_num[[df_num.columns[i], 'SalePrice']]
    tmpDf = tmpDf[tmpDf[df_num.columns[i]] != 0]
    individual_features_df.append(tmpDf)
    
all_correlations = {feature.columns[0]: feature.corr()['SalePrice'][0] for feature in individual_features_df}
all_correlations = sorted(all_correlations.items(), key=operator.itemgetter(1))

for (key, value) in all_correlations:
    print("{:>15}: {:>15}".format(key, value))
 KitchenAbvGr: -0.13920069217785566
     HalfBath: -0.08439171127179887
   MSSubClass: -0.08428413512659523
  OverallCond: -0.0778558940486776
       YrSold: -0.028922585168730426
 BsmtHalfBath: -0.028834567185481712
     PoolArea: -0.014091521506356928
 BsmtFullBath: 0.011439163340408634
       MoSold: 0.04643224522381936
    3SsnPorch: 0.06393243256889079
  OpenPorchSF: 0.08645298857147708
      MiscVal: 0.08896338917298924
   Fireplaces: 0.1216605842136395
    BsmtUnfSF: 0.16926100049514192
 BedroomAbvGr: 0.18093669310849045
   WoodDeckSF: 0.19370601237520677
   BsmtFinSF2: 0.19895609430836586
EnclosedPorch: 0.2412788363011751
  ScreenPorch: 0.25543007954878405
      LotArea: 0.2638433538714063
 LowQualFinSF: 0.3000750165550133
  LotFrontage: 0.35179909657067854
   MasVnrArea: 0.4340902197568926
   BsmtFinSF1: 0.4716904265235731
  GarageYrBlt: 0.48636167748786213
 YearRemodAdd: 0.5071009671113867
    YearBuilt: 0.5228973328794967
 TotRmsAbvGrd: 0.5337231555820238
     FullBath: 0.5745626737760816
     1stFlrSF: 0.6058521846919166
   GarageArea: 0.6084052829168343
  TotalBsmtSF: 0.6096808188074366
   GarageCars: 0.6370954062078953
     2ndFlrSF: 0.6733048324568383
    GrLivArea: 0.7086244776126511
  OverallQual: 0.7909816005838047

Conclusion

The most strongly correlated values are as follows in the golden_features_list.

1
2
golden_features_list = [key for key, value in all_correlations if abs(value) >= 0.5]
print("Following are the top {} strongly correlated values with SalePrice:\n{}".format(len(golden_features_list), golden_features_list))
Following are the top 11 strongly correlated values with SalePrice:
['YearRemodAdd', 'YearBuilt', 'TotRmsAbvGrd', 'FullBath', '1stFlrSF', 'GarageArea', 'TotalBsmtSF', 'GarageCars', '2ndFlrSF', 'GrLivArea', 'OverallQual']

Feature to Feature Relationship

1
2
3
4
5
6
corr = df_num.drop('SalePrice', axis=1).corr()
plt.figure(figsize=(12, 10))

sns.heatmap(corr[(corr >= 0.5) | (corr <= -0.4)],
            cmap='viridis', vmax=1.0, vmin=-1.0, linewidths=0.1,
            annot=True, annot_kws={"size": 8}, square=True);

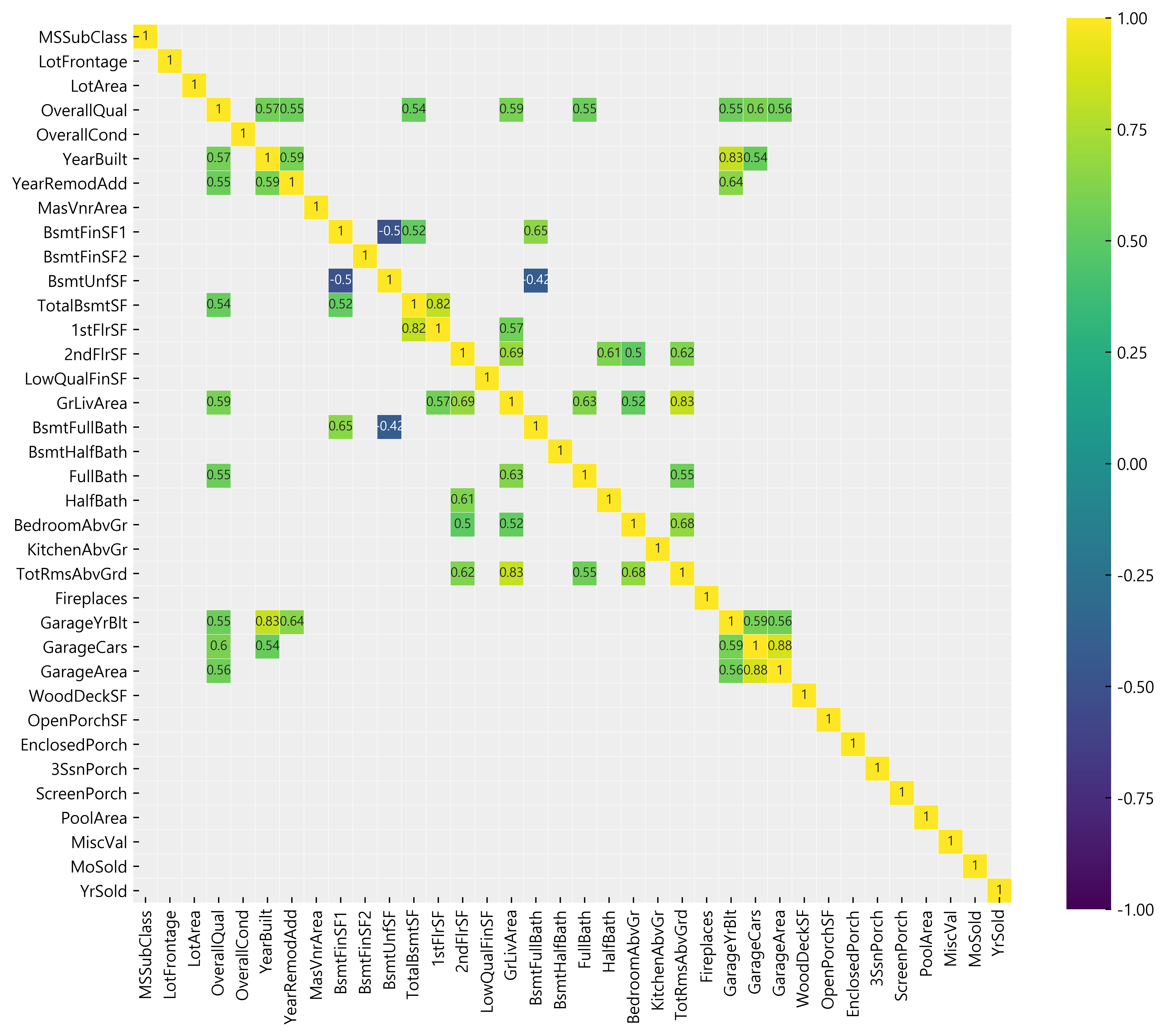
EDA_Practice_-_HousePrices_25_0


Q –> Q (Quantitative to Quantitative relationship)

1
2
3
4
5
6
7
quantitative_features_list = ['LotFrontage', 'LotArea', 'MasVnrArea', 'BsmtFinSF1', 'BsmtFinSF2', 'TotalBsmtSF', '1stFlrSF',
    '2ndFlrSF', 'LowQualFinSF', 'GrLivArea', 'BsmtFullBath', 'BsmtHalfBath', 'FullBath', 'HalfBath',
    'BedroomAbvGr', 'KitchenAbvGr', 'TotRmsAbvGrd', 'Fireplaces', 'GarageCars', 'GarageArea', 'WoodDeckSF', 'OpenPorchSF', 
    'EnclosedPorch', '3SsnPorch', 'ScreenPorch', 'PoolArea', 'MiscVal', 'SalePrice']

df_quantitative_values = df[quantitative_features_list]
df_quantitative_values.head()

LotFrontage LotArea MasVnrArea BsmtFinSF1 BsmtFinSF2 TotalBsmtSF 1stFlrSF 2ndFlrSF LowQualFinSF GrLivArea ... GarageCars GarageArea WoodDeckSF OpenPorchSF EnclosedPorch 3SsnPorch ScreenPorch PoolArea MiscVal SalePrice
0 65.0 8450 196.0 706 0 856 856 854 0 1710 ... 2 548 0 61 0 0 0 0 0 208500
1 80.0 9600 0.0 978 0 1262 1262 0 0 1262 ... 2 460 298 0 0 0 0 0 0 181500
2 68.0 11250 162.0 486 0 920 920 866 0 1786 ... 2 608 0 42 0 0 0 0 0 223500
3 60.0 9550 0.0 216 0 756 961 756 0 1717 ... 3 642 0 35 272 0 0 0 0 140000
4 84.0 14260 350.0 655 0 1145 1145 1053 0 2198 ... 3 836 192 84 0 0 0 0 0 250000

5 rows × 28 columns

1
2
3
features_to_analyse = [x for x in quantitative_features_list if x in golden_features_list]
features_to_analyse.append('SalePrice')
features_to_analyse
['TotalBsmtSF',
 '1stFlrSF',
 '2ndFlrSF',
 'GrLivArea',
 'FullBath',
 'TotRmsAbvGrd',
 'GarageCars',
 'GarageArea',
 'SalePrice']

The Distribution

1
2
3
4
5
fig, ax = plt.subplots(round(len(features_to_analyse) / 3), 3, figsize= (18, 12))

for i, ax in enumerate(fig.axes):
    if i < len(features_to_analyse) - 1:
        sns.regplot(x = features_to_analyse[i], y='SalePrice', data=df[features_to_analyse], ax=ax)

EDA_Practice_-_HousePrices_31_0

We can see that features such as TotalBsmtSF, 1stFlrSF, GrLivArea have a big spread but I cannot tell what insights this information gives us


C -> Q (Categorical to Quantitative Relationship)

1
2
3
4
# quantitative_features_list[:-1] as the last column is SalePrice and we want to keep it
categorical_features = [a for a in quantitative_features_list[:-1] + df.columns.tolist() if (a not in quantitative_features_list[:-1]) or (a not in df.columns.tolist())]
df_categ = df[categorical_features]
df_categ.head()

MSSubClass MSZoning Street LotShape LandContour Utilities LotConfig LandSlope Neighborhood Condition1 ... GarageYrBlt GarageFinish GarageQual GarageCond PavedDrive MoSold YrSold SaleType SaleCondition SalePrice
0 60 RL Pave Reg Lvl AllPub Inside Gtl CollgCr Norm ... 2003.0 RFn TA TA Y 2 2008 WD Normal 208500
1 20 RL Pave Reg Lvl AllPub FR2 Gtl Veenker Feedr ... 1976.0 RFn TA TA Y 5 2007 WD Normal 181500
2 60 RL Pave IR1 Lvl AllPub Inside Gtl CollgCr Norm ... 2001.0 RFn TA TA Y 9 2008 WD Normal 223500
3 70 RL Pave IR1 Lvl AllPub Corner Gtl Crawfor Norm ... 1998.0 Unf TA TA Y 2 2006 WD Abnorml 140000
4 60 RL Pave IR1 Lvl AllPub FR2 Gtl NoRidge Norm ... 2000.0 RFn TA TA Y 12 2008 WD Normal 250000

5 rows × 49 columns


non-numerical features

1
2
df_not_num = df_categ.select_dtypes(include = ['O']) # Object(O)
print('There are {} non numerical features including:\n{}'.format(len(df_not_num.columns), df_not_num.columns.tolist()))
There are 39 non numerical features including:
['MSZoning', 'Street', 'LotShape', 'LandContour', 'Utilities', 'LotConfig', 'LandSlope', 'Neighborhood', 'Condition1', 'Condition2', 'BldgType', 'HouseStyle', 'RoofStyle', 'RoofMatl', 'Exterior1st', 'Exterior2nd', 'MasVnrType', 'ExterQual', 'ExterCond', 'Foundation', 'BsmtQual', 'BsmtCond', 'BsmtExposure', 'BsmtFinType1', 'BsmtFinType2', 'Heating', 'HeatingQC', 'CentralAir', 'Electrical', 'KitchenQual', 'Functional', 'FireplaceQu', 'GarageType', 'GarageFinish', 'GarageQual', 'GarageCond', 'PavedDrive', 'SaleType', 'SaleCondition']

“Looking at these features we can see that a lot of them are of the type Object(O). In our data transformation notebook we could use Pandas categorical functions (equivalent to R’s factor) to shape our data in a way that would be interpretable for our machine learning algorithm. ExterQual for instace could be transformed to an ordered categorical object.”

Definitely need more study on this especially on the transformation of data

1
2
3
4
plt.figure(figsize= (10, 6))
ax = sns.boxplot(x='BsmtExposure', y='SalePrice', data=df_categ)
plt.setp(ax.artists, alpha=.5, linewidth=2, edgecolor="k")
plt.xticks(rotation=45)
(array([0, 1, 2, 3]), <a list of 4 Text xticklabel objects>)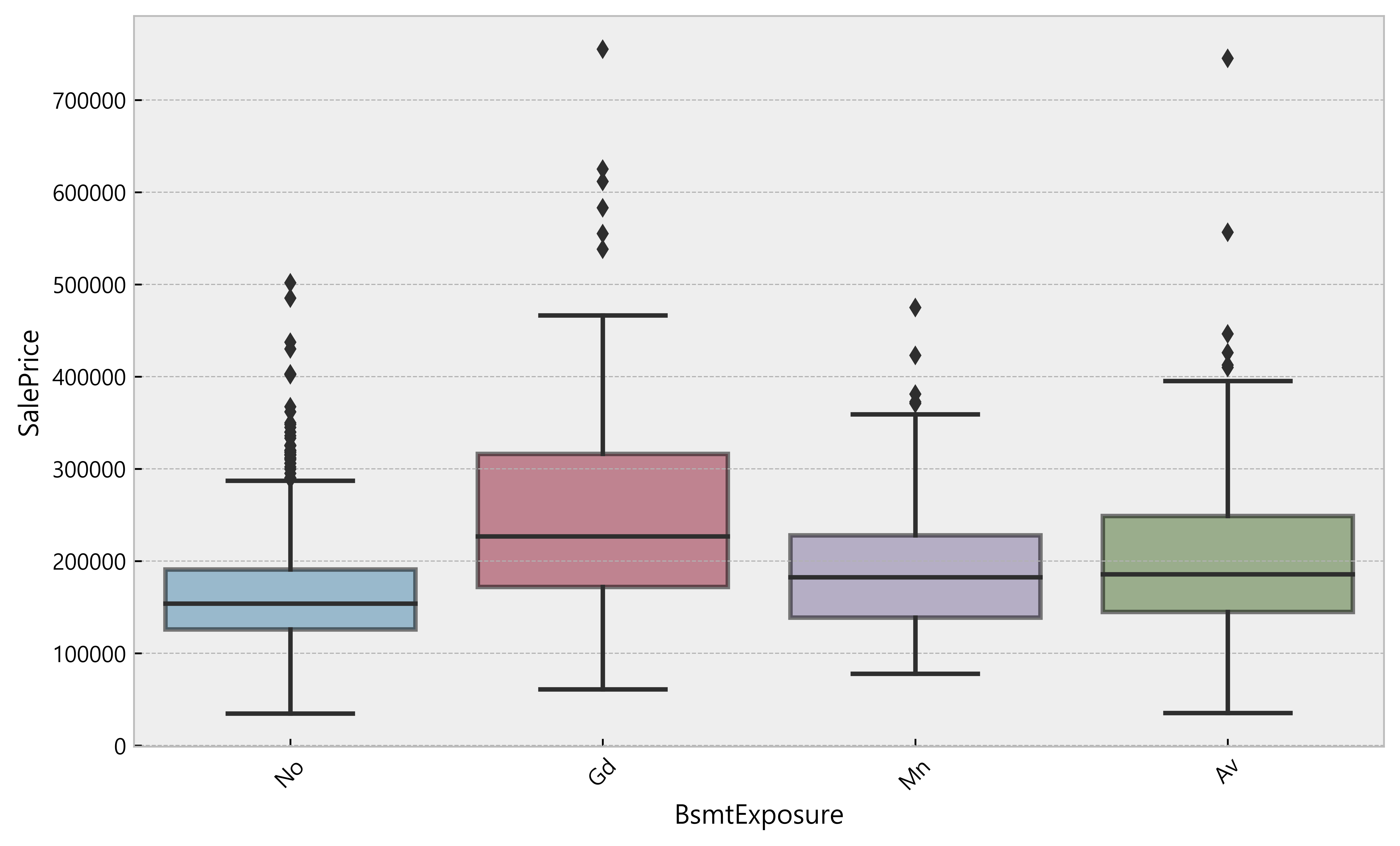

EDA_Practice_-_HousePrices_37_1

1
2
3
4
plt.figure(figsize= (12, 6))
ax = sns.boxplot(x='SaleCondition', y='SalePrice', data=df_categ)
plt.setp(ax.artists, alpha=.5, linewidth=2, edgecolor="k")
plt.xticks(rotation=45)
(array([0, 1, 2, 3, 4, 5]), <a list of 6 Text xticklabel objects>)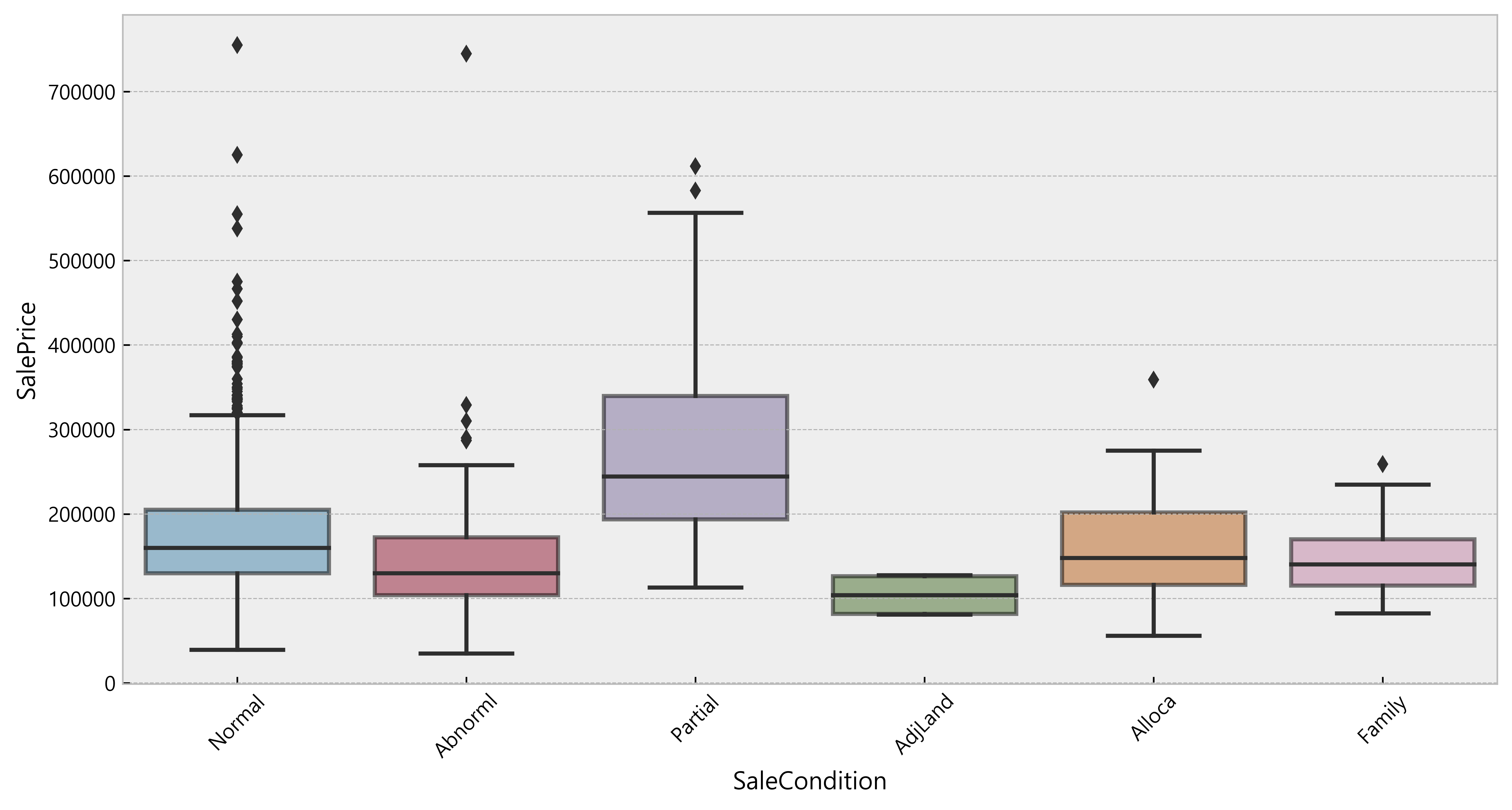

EDA_Practice_-_HousePrices_38_1

1
2
3
4
5
6
7
8
fig, axes = plt.subplots(round(len(df_not_num.columns) / 3), 3, figsize=(12, 30))

for i, ax in enumerate(fig.axes):
    if i < len(df_not_num.columns):
        ax.set_xticklabels(ax.xaxis.get_majorticklabels(), rotation=45)
        sns.countplot(x=df_not_num.columns[i], alpha=0.7, data=df_not_num, ax=ax)
        
fig.tight_layout()

EDA_Practice_-_HousePrices_39_0


Deduction

Some categories are predominant for some features
e.g. Utilities, Heating, etc.